회귀 분석
회귀 분석이란?
- 종속변수(Y)와 하나 이상의 독립변수(X) 간의 관계를 추정하여 연속형 종속변수를 예측하는 통계/머신러닝 기법
- 지도학습에서의 분류(Classification)와 회귀(Regression)의 차이
- 분류: 결과값이 이산형(클래스 라벨)
- 회귀: 결과값이 연속형(숫자 값)
회귀모델을 사용하는 이유
- 미래 값 예측: 판매량, 주가, 온도 등 실수값 예측에 사용
- 인과 관계 해석(통계적 관점): 특정 독립변수가 종속변수에 미치는 영향력을 해석하기 위해
- 데이터 기반 의사결정: 추세(Trend) 파악, 자원 배분 등
선형 회귀의 4대 기본 가정
- 선형성(Linearity)
- 종속변수(y)와 독립변수(x) 사이의 관계가 직선 형태여야 한다는 가정
- 산점도(Scatter Plot)를 그렸을 때 데이터가 직선의 흐름을 보이는지 확인하거나, 잔차 그래프(Residual Plot)에서 잔차들이 0을 중심으로 무작위로 퍼져 있는지 확인
- 독립성(Independence)
- 오차(Residual)들 사이에 상관관계가 없어야 한다는 가정
- 등분산성(Homoscedasticity)
- 오차의 분산이 모든 독립변수 값에 대해 일정해야 한다는 가정
- 정규성(Normality)
- 오차항이 평균이 0인 정규분포를 따라야 한다는 가정
- Q-Q Plot을 그려서 점들이 직선 위에 놓이는지 확인하거나, Shapiro-Wilk 검정 등을 수행
선형 회귀(Linear Regression)
개념
- 가정
- 독립변수(X)와 종속변수(Y)가 선형적(일차 방정식 형태)으로 관계를 맺고 있다고 가정회귀식

- β0: 절편(intercept)
- βi: 각 독립변수의 회귀계수(coefficient)
- 독립변수(X)와 종속변수(Y)가 선형적(일차 방정식 형태)으로 관계를 맺고 있다고 가정회귀식
- 장점
- 해석이 간단, 구현이 쉬움
- 단점
- 데이터가 선형성이 아닐 경우 예측력이 떨어짐
import pandas as pd
import numpy as np
from sklearn.linear_model import LinearRegression, SGDRegressor
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error, r2_score
# LinearRegression(정규 방정식)
X = df.drop('타겟 변수', axis=1)
y = df['타겟 변수']
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.2, random_state=42)
linear = LinearRegression()
linear.fit(X_train, y_train)
y_pred = linear.predict(X_test)
mse_lin = mean_squared_error(y_test, y_pred)
r2_lin = r2_score(y_test, y_pred)
# SGDRegressor(경사 하강법)
sgd_reg = SGDRegressor(max_iter=6000, random_state=42)
sgd_reg.fit(X_train, y_train)
y_pred = sgd_reg.predict(X_test)
mse_sgd = mean_squared_error(y_test, y_pred)
r2_sgd = r2_score(y_test, y_pred)
다항 회귀(Polynomial Regression)
개념
- 비선형적인 관계를 다항식 형태로 모델링
- n차 다항식(n≥2)

- 단순 선형항(X)뿐만 아니라 X2, X3,... 같은 고차항을 추가해 비선형 패턴을 학습할 수 있음
주의점
- 고차항을 무작정 늘리면 훈련 데이터에 과도하게 맞춰져 과적합(overfitting) 문제가 발생할 수 있음
- 모델 복잡도와 일반화 성능 간의 균형을 맞춰야 함
import pandas as pd
import numpy as np
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import PolynomialFeatures
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error, r2_score
from sklearn.pipeline import Pipeline
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
lin_reg = LinearRegression()
lin_reg.fit(X_train, y_train)
y_pred = lin_reg.predict(X_test)
mse_lin = mean_squared_error(y_test, y_pred)
r2_lin = r2_score(y_test, y_pred)
poly_model = Pipeline([
("poly", PolynomialFeatures(degree=2, include_bias=False)),
("lin_reg", LinearRegression())
])
poly_model.fit(X_train, y_train)
y_pred = poly_model.predict(X_test)
회귀 모델 평가 방법
MSE(Mean Squared Error)
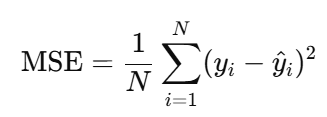
- 예측값과 실제값의 차이를 제곱하여 평균
- 오차가 클수록 제곱에 의해 더 큰 벌점이 매겨지므로 큰 오차에 특히 민감
MAE(Mean Absolute Error)

- 예측값과 실제값의 차이를 절댓값으로 측정한 후 평균
- 예측이 평균적으로 실제값에서 얼마나 벗어났는지 직관적으로 표현
RMSE(Root Mean Squared Error)

- MAE와 달리 제곱을 통해 큰 오차에 가중치를 더 주는 특징
- 오차가 클수록 패널티가 커지므로 큰 오차가 중요한 문제에서 자주 사용
R2(결정 계수)

- 값의 범위
- 0 ~ 1
- 해석
- 1에 가까울수록 학습된 모델이 데이터를 잘 설명한다고 봄
- 0이라면 모델이 종속변수를 전혀 설명하지 못한다는 의미
고급 회귀 기법 - Lasso & Ridge Regression
Ridge(릿지) 회귀

- 가중치 제곱합(L2 Norm)을 페널티로 추가
- 효과: 가중치가 너무 커지지 않도록 방지(가중치 값을 부드럽게 줄임)
Lasso(라쏘) 회귀

- 가중치 절대값합(L1 Norm)을 페널티로 추가
- 효과: 가중치를 0으로 만들어 변수 선택(Feature Selection) 효과
import pandas as pd
import numpy as np
from sklearn.datasets import fetch_california_housing
from sklearn.model_selection import train_test_split
from sklearn.linear_model import Ridge, Lasso
from sklearn.metrics import mean_squared_error, r2_score
X = 타겟을 제외한 변수
y = 타겟 변수
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
ridge_reg = Ridge(alpha=1.0, random_state=42)
ridge_reg.fit(X_train, y_train)
y_pred = ridge_reg.predict(X_test)
mse_ridge = mean_squared_error(y_test, y_pred)
r2_ridge = r2_score(y_test, y_pred)
lasso_reg = Lasso(alpha=1.0, random_state=42, max_iter=10000)
lasso_reg.fit(X_train, y_train)
y_pred = lasso_reg.predict(X_test)
mse_lasso = mean_squared_error(y_test, y_pred)
r2_lasso = r2_score(y_test, y_pred)'머신러닝' 카테고리의 다른 글
| 스케일링(Scaling) (0) | 2025.12.01 |
|---|---|
| 인코딩(Encoding) (0) | 2025.12.01 |
| 지도학습 & 비지도학습 (0) | 2025.11.28 |