✅ 오늘 한 것
통계 & 머신러닝 개인 과제, 졸업 시험
✏️ 오늘 배운 점
머신러닝 특강
로지스틱 선형회귀가 왜 분류 모델인가?
로지스틱 회귀는 선형회귀처럼 데이터를 선형식으로 모델링하지만 출력값을 시그모이드 함수를 통해 확률(0~1) 로 변환하고 그 확률을 기준으로 이진 분류를 수행하기 때문에 “분류 모델” 입니다.
회귀: rmse, rma, mse 등 평가 지표
분류: 혼동 행렬(Confusion Matrix)

cm = confusion_matrix(y_test, y_pred_test)
tn, fp, fn, tp = cm.ravel()
정밀도 precision_manual = tp / (tp + fp)
민감도(재현율) recall_manual = tp / (tp + fn)
f1-Score: 정밀도와 재현율의 조화 평균
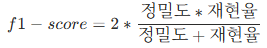
f1_manual = 2 * (precision_manual * recall_manual) / (precision_manual + recall_manual)
정확도(Accuracy)

accuracy_manual = (tp + tn) / (tp + tn + fp + fn)
accuracy_sklearn = accuracy_score(y_test, y_pred_test)
ROC 커브: 모든 임계값에서의 모델 성능을 한눈에 보여주는 강력한 시각화 도구
ROC (Receiver Operating Characteristic) 커브
- X축: False Positive Rate (FPR) = FP / (FP + TN)
- "실제 음성인 것들 중에서 모델이 양성이라고 잘못 예측한 비율"을 의미합니다.
- Y축: True Positive Rate (TPR) = TP / (TP + FN) = Recall
- 실제 양성인 것들 중에서 모델이 양성이라고 올바르게 예측한 비율"을 의미합니다.
ROC 커브가 중요한 이유
- 임계값 독립적: 다양한 임계값에서의 성능을 모두 고려
- 모델 비교 용이: 여러 모델의 성능을 한 그래프에서 비교 가능
- 비즈니스 의사결정: TPR과 FPR 트레이드오프를 고려한 임계값 선택
졸업 시험
열역학 제 0법칙: 같은 온도에서 A=B, B=C면, A=C이다.
열역학 제 1법칙: 고립계에서 에너지의 총합은 일정하다.
열역학 제 2법칙: 고립계에서 엔트로피는 증가하는 방향으로 진행된다.
열역학 제 3법칙: 절대 온도 0K에서 엔트로피는 0에 수렴한다.
엔트로피 --> S=q/T = KlnW
고립계에서 엔트로피는 증가하는 방향으로 진행된다.
✏️ 오늘의 핵심
오늘은 로지스틱 회귀(Logistic Regression) 가 분류 모델로 작동하는 원리와 그 성능을 평가하는 다양한 분류 지표(metric) 들을 학습했습니다.
📌추가로 해야할 점
졸업 시험, 통계 & 머신러닝 복습
'품질관리(QAQC) 데이터 부트캠프(본캠프)' 카테고리의 다른 글
| 본캠프_8주차(목)_TIL(2차 프로젝트 시작) (0) | 2025.11.06 |
|---|---|
| 본캠프_8주차(수)_TIL(랜덤 포레스트, XGBoost 정리) (0) | 2025.11.05 |
| 본캠프_8주차(월)_TIL (0) | 2025.11.03 |
| 본캠프_7주차(금)_TIL (0) | 2025.10.31 |
| 본캠프_7주차(목)_TIL(머신러닝 정리) (0) | 2025.10.30 |