✅ 오늘 한 것
실무에 쓰는 머신러닝 기초(클러스터링, 차원 축소), AI 서비스 개발
✏️ 오늘 배운 점
실무에 쓰는 머신러닝 기초
비지도 학습
- 정답(Label) 없이 데이터에서 패턴이나 구조를 찾는 머신 러닝 기법
- 활용 영역
- 데이터의 군집화(Clustering)
- 차원 축소(Dimensionality Reduction)
- 이상치 탐지(Anomaly Detection) 등
- Label 대신 데이터 자체의 유사성과 패턴에 집중
군집 분석
- 비슷한 특성을 가진 데이터들을 묶어서(Cluster) 각 그룹 내 데이터들끼리의 유사도를 최대화하고, 다른 그룹과의 차이는최대화하는 기법
- 목적
- 데이터의 구조 파악
- 정답 없이 데이터의 자연스러운 분포 확인
- 세분화(Segmentation)
- 마케팅에서는 고객 세분화, 제조업에서는 센서 데이터로 기계 작동 패턴 분류 등 수행
- 데이터의 구조 파악
군집 분석의 절차
- 데이터 수집 및 전처리
- 이상치 제거, 결측치 처리, 스케일링/정규화
- 군집 수 또는 파라미터 설정
- K-Means의 경우 k 설정, DBSCAN은 거리(ε), 최소 데이터 수(minPts) 등
- 군집화 알고리즘 적용
- 설정에 따라 알고리즘 수행
- 결과 해석 및 평가
- 실루엣 계수 등 군집 평가 지표 활용
- 사후 활용
- 마케팅 전략, 제품 개선, 이상치 탐지 등
주요 군집 분석 알고리즘
- K-Means

- 알고리즘 개요
- 미리 군집 수 k를 지정해야 함
- 무작위로 k개의 중심을 선택 후 각 데이터 포인트를 가장 가까운 중심에 할당
- 각 군집의 중심을 다시 계산하고 재할당하는 과정 반복
- 군집 내 데이터와 중심 간 거리의 제곱합 최소화
- 장점
- 계산 속도가 빠르고 구현이 간단
- 대용량 데이터에도 비교적 잘 작동
- 단점
- 군집 수 k를 미리 알아야 함
- 이상치에 취약(중심값에 영향을 미침)
- 구형 구조가 아닌 복잡한 형태의 분포를 파악하기 어려움
- 알고리즘 개요
- DBSCAN

- 알고리즘 개요
- 밀도 기반 군집화 기법.
- 일정 거리(ε) 내 데이터가 많으면(최소 포인트 수 minPts 이상) 그 영역을 밀도가 높다고 판단해 하나의 군집으로 결정
- k를 미리 설정하지 않아도 되며, 노이즈 포인트(어느 군집에도 속하지 않는 점)을 구분할 수 있음
- 장점
- 군집 수를 사전에 알 필요가 없음
- 노이즈와 이상치를 자연스럽게 처리
- 구형이 아닌 복잡한 형태의 군집도 잘 찾아냄
- 단점
- 파라미터 ε와 minPts에 민감
- 데이터 밀도가 균일하지 않으면 성능이 떨어질 수 있음
- 알고리즘 개요
- 계층적 클러스터링

- 알고리즘 개요
- 데이터 포인트 각각이 하나의 군집으로 시작 → 유사도가 가장 높은 군집들끼리 병합 → 최종적으로 하나의 군집 형성
- 하나의 군집에서 시작해 분할해 나가는 방법도 있음(분할적 접근)
- 덴드로그램으로 시각화 가능
- 장점
- 군집의 계층적 구조 파악이 쉬움(덴드로그램)
- 군집 수를 명확히 결정하지 않아도 덴드로그램의 특정 높이에 따라 유연하게 군집 개수 결정 가능
- 단점
- 계산 복잡도가 높아서 대규모 데이터에 적용하기 어려움
- 알고리즘 개요
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn.cluster import KMeans, DBSCAN, AgglomerativeClustering
from sklearn.model_selection import train_test_split
from sklearn.metrics import silhouette_score
from sklearn.decomposition import PCA
X = df.data
y = df.target
# K-Means
kmeans = KMeans(n_clusters=3, random_state=42)
kmeans_labels = kmeans.fit_predict(X)
# DBSCAN
dbscan = DBSCAN(eps=0.5, min_samples=5)
dbscan_labels = dbscan.fit_predict(X)
# 계층적 클러스터링
agg = AgglomerativeClustering(n_clusters=3)
agg_labels = agg.fit_predict(X)
# 각 군집 결과의 실루엣 지수
kmeans_sil = silhouette_score(X, kmeans_labels)
dbscan_sil = silhouette_score(X, dbscan_labels)
agg_sil = silhouette_score(X, agg_labels)
# PCA로 차원 축소 (2차원)
pca = PCA(n_components=2)
X_pca = pca.fit_transform(X)
fig, axes = plt.subplots(1, 3, figsize=(15, 4))
# K-Means 시각화
axes[0].scatter(X_pca[:, 0], X_pca[:, 1], c=kmeans_labels)
axes[0].set_title("K-Means")
# DBSCAN 시각화
axes[1].scatter(X_pca[:, 0], X_pca[:, 1], c=dbscan_labels)
axes[1].set_title("DBSCAN")
# Agglomerative 시각화
axes[2].scatter(X_pca[:, 0], X_pca[:, 1], c=agg_labels)
axes[2].set_title("Agglomerative")
plt.tight_layout()
plt.show()
군집 분석 평가 방법
- 실루엣 계수
- 각 데이터 포인트의 응집도(a)와 분리도(b)를 이용해 계산
- 응집도(a): 같은 군집 내 데이터와의 평균 거리
- 분리도(b): 가장 가까운 다른 군집과의 평균 거리
- 계산 공식
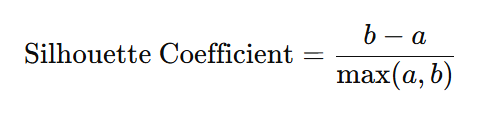
- 범위
- -1 ~ 1
- 1에 가까울수록 해당 데이터가 잘 군집되었음을 의미
- 0 근처면 군집 경계에 위치
- 0보다 작으면 잘못된 군집화 가능성
- 각 데이터 포인트의 응집도(a)와 분리도(b)를 이용해 계산
- Davies-Bouldin Index
- 군집 내 분산과 군집 간 거리의 비율을 활용
- 각 군집에 대해 다른 군집과의 거리를 비교하면서 군집끼리 얼마나 겹치는지 측정
- 범위
- 0 이상
- 값이 0에 가까울수록 군집 간 구분이 잘 되어 있음
- 값이 커질수록 군집 간 겹침이 많아 군집화 품질이 낮음
- 군집 내 분산과 군집 간 거리의 비율을 활용
- 내부 평가 vs. 외부평가
- 내부 평가
- 데이터 내부의 정보(분산, 거리 등)를 활용해 평가 (실루엣 계수, Davies-Bouldin Index 등)
- 외부 평가
- 이미 알려진 정답(Label)과 군집 결과를 비교(정답이 있을 때만 가능)
- 내부 평가
차원 축소의 필요성
- 고차원 데이터란?
- 데이터의 피처(변수)가 매우 많은 상태
- 어떤 문제가 생길까?
- 모델 학습 시 연산 복잡도가 급증하여 시간이 오래 걸림
- 많은 피처들 중 일부는 실제로 중요한 정보를 주지 못하는 노이즈(잡음)일 수 있음
- 차원이 너무 높아지면 데이터를 시각화하기가 어려워 패턴 파악이 힘듬
- 차원 축소의 장점
- 노이즈 제거로 모델 성능 및 일반화 능력을 개선할 수 있음
- 2차원이나 3차원으로 축소하면 시각적으로 직관적인 분석을 할 수 있음
- 데이터의 핵심 구조나 패턴을 더 쉽게 발견할 수 있음
선형 차원 축소 vs. 비선형 차원 축소
- 선형 차원 축소
- 데이터를 특정 선형 변환으로 투영하여 차원을 줄이는 기법(PCA)
- 비선형 차원 축소
- 데이터가 복잡한 기하학적 구조를 가질 때 선형 변환만으로는 충분치 않을 수 있으므로 비선형 맵핑을 이용(t-SNE, UMAP 등)
차원 축소와 노이즈 제거
- 대부분의 데이터에는 잡음이 포함되어 있음
- 차원 축소 시 중요한 변동을 잘 설명하지 못하는 데이터는 줄여버림으로써 불필요한 정보를 걸러낼 수 있음
PCA (주성분 분석)
- 핵심 아이디어
- 데이터에서 가장 분산이 큰 방향(주성분)을 찾아 그 방향으로 데이터를 투영하면 그 축이 데이터의 중요한 변동(variance)을 많이 설명할 수 있음
- 주성분
- 가장 큰 분산을 갖는 방향을 1주성분으로 그 다음으로 큰 분산을 갖는 서로 직교(90도)하는 방향을 2주성분으로 하는 식으로 이어짐
- 설명 분산 비율
- 몇 개의 주성분만으로 전체 분산의 몇 퍼센트를 설명할 수 있는지 나타냄
- 장점
- 계산이 비교적 간단(선형 연산), 결과 해석이 용이(주성분 방향 해석 가능), 노이즈 제거 효과
- 단점
- 데이터가 선형이 아닌 패턴일 경우 정보 손실이 발생할 수 있음, 매우 복잡한 구조를 충분히 반영하기 어려움
t-SNE (t-Distributed Stochastic Neighbor Embedding)

- 고차원 공간에서 서로 가까운 데이터 포인트는 가까이, 먼 데이터 포인트는 멀리 배치하려고 하는 비선형 차원 축소 기법
- 동작 원리
- 고차원에서 데이터 간 지역적 확률 분포 추정(주변 데이터와의 거리 기반)
- 2차원 혹은 3차원에서 비슷한 확률 분포가 되도록 데이터 배치
- 장점
- 데이터의 군집이 자연스럽게 시각화되어 군집별 패턴을 인지하기 쉬움
- 단점
- 계산 비용이 큰 편
- 하이퍼파라미터 선태겡 따라 결과가 달라질 수 있음
- 시각화 결과 해석이 직관적이지만, 실제 거리 척도가 왜곡될 수 있으니 주의
UMAP (Uniform Manifold Approximation and Projection)

- t-SNE와 유사하게 고차원 데이터의 구조를 2D/3D로 매핑하는 비선형 차원 축소 기법.
- 장점
- t-SNE보다 빠르고 대규모 데이터에도 비교적 효율적임
- 지역적/글로벌 구조를 함께 잘 반영함
- 매개변수를 통해 클러스터의 응집도나 분산 정도를 조절할 수 있음
- 단점
- 알고리즘의 개념이 비교적 복잡하고, 하이퍼파라미터 튜닝을 요함
- t-SNE만큼은 아니지만 여전히 축소 과정에서 정보 왜곡이 발생할 수 있음
이상 탐지(Anomaly Detection)란?
- 데이터에서 정상 패턴과 크게 다른 행위를 보이는 특이한 패턴(이상, Anomaly)을 찾는 기법
이상치 탐지(Outlier Detection)와의 차이
- 이상치 탐지(Outlier Detection): 단순히 통계적으로 극단값을 찾는 데 초점
- 이상 탐지(Anomaly Detection): 단순 극단값 뿐 아니라 맥락이나 시계열 상의 패턴을 함께 고려하여 비정상인지 판단
주요 이상 탐지 알고리즘
- One-Class SVM

- 알고리즘 원리
- SVM은 이진 분류를 위해 고안된 알고리즘이지만, One-Class SVM은 단 하나의 클래스(정상 클래스)만을 학습해 해당 클래스 영역을 정의함
- 정상 데이터가 분포하는 공간 주위에 경계를 형성하고 경계 밖에 있는 데이터는 비정상으로 분류함
- 특징
- 고차원 공간에서도 비교적 잘 동작할 수 있음(커널 함수의 사용)
- 데이터
- 알고리즘 원리
- Isolation Forest

- 알고리즘 원리
- Isolation Forest는 랜덤 포레스트와 유사한 아이디어에 기반
- 이상치는 전체 데이터 중 상대적으로 적고 특정 속성값에서 극단적인 위치를 차지하는 경우가 많다는 가정 하에 무작위로 특성과 분할값을 골라 데이터를 계속 나누어가는 과정에서 쉽게 분리되는 데이터는 이상일 가능성이 높다고 판단
- 특징
- 랜덤 포레스트 방식으로 여러 개의 무작위 트리를 구성하고, 각 트리에서 한 데이터가 분리되는 깊이를 측정하여 이상 점수 부여
- 대규모 데이터셋에서도 빠르게 동작
- 구현이 간단하고 직관적임
- 알고리즘 원리
AI 서비스 개발
Vibe Coding: 무엇을 만들 것인가에 집중하여 AI와 자연어로 코딩하는 새로운 패러다임
Zero Python: 오직 브라우저(Client-side) 기술만으로 동적인 기술을 구현하는 방법론
웹페이지의 구성 요소
- HTML(구조): 웹페이지의 뼈대 (제목, 버튼, 입력창)
- CSS(스타일): 인테리어와 디자인 (반응형 레이아웃, 색상)
- Javascript(동작): 스위치와 기능 (클릭 시 반응, 데이터 계산)
PRD(Product Requirements Document)란?
- 개발 전 '무엇을, 왜, 어떻게' 만들지 정의하는 제품 요구 사항 정의서
- AI 코딩 실패의 주원인 = 모호한 지시(Prompt)
- 내 머릿속의 추상적인 아이디어를 AI가 이해하기 쉬운 구체적인 개발 문서로 변환하는 과정
- PRD 항목
- 프로젝트 배경 및 목적 (Background & Objectives)
- 타겟 유저 (Target Audience)
- 데이터 시각화 및 기능 요구사항 (Functional Requirements)
- 데이터 로직 및 알림 (Data Logic & Alerts)
- 기술적 요구사항 (Technical Requirements)
✏️ 오늘의 질문
1. K-Means와 DBSCAN 중 어느 것을 골라야 하는가?
K-Means: 군집 수를 알고 있거나 대략적인 예상이 가능한 경우
DBSCAN: 군집이 구형 형태가 아닐 수 있거나 노이즈 처리가 중요한 경우
2. 실제 데이터에서는 이상치나 결측치 처리를 어떻게 해야 하는가?
군집 분석 전에 결측치 처리, 스케일링(정규화), 이상치 처리(제거 혹은 적절한 대체)를 선행해야 한다.
특히, K-Means는 평균값에 민감해 이상치 영향을 크게 받으므로 사전에 주의 필요하다.
3. PCA와 t-SNE(또는 UMAP)의 가장 큰 차이는 무엇인가?
PCA: 선형 변환을 이용해 분산이 가장 큰 축을 찾는 방식으로 차원을 줄임
t-SNE or UMAP: 비선형 방식으로 근접한 데이터들을 가깝게 배치해 2D/3D 시각화에 더욱 적합
4. 커널 함수란?
SVM 같은 알고리즘에서 복잡한 비선형 데이터를 선형으로 분리하기 위해 사용하는 수학적 기법
📌추가로 해야 할 점
실무에 쓰는 머신러닝 기초(이상 탐지, 딥러닝)
'품질관리(QAQC) 데이터 부트캠프(본캠프)' 카테고리의 다른 글
| 본캠프_16주차(월)_TIL(최종 프로젝트 주제 선정) (1) | 2025.12.29 |
|---|---|
| 본캠프_15주차(금)_TIL(딥러닝, 고민해결소) (0) | 2025.12.26 |
| 본캠프_15주차(화)_TIL(앙상블 기법, 베이직, 스탠다드) (0) | 2025.12.23 |
| 본캠프_15주차(월)_TIL(분류, 베이직) (0) | 2025.12.22 |
| 본캠프_14주차(금)_TIL(회귀, 스탠다드) (0) | 2025.12.19 |